Technical

This page attempts to describe the internal workings of SAM in "somewhat" human-readable fashion. It assumes you are familiar with the concepts of time and arithmetic! It assumes you know (or can reference) SAM's phonemes. It assumes you are familiar with programming concepts in general, but no specific knowledge of the Commodore 128, 6502 ML, nor BASIC is required. The reader should also be familiar with simple audio concepts like amplitude, frequency, phase, power, and wavelength. Knowing some phonetic terms (like diphthong and plosive) would help, but see the main SAM documentation if you need more info on these terms. Familiarity with digital sampling and playback would also be helpful, but not strictly required. (This page is mainly notes for myself, but you may find it useful!)

Reciter is an extra layer on top of SAM, so SAM is analyzed first.

Theory

Before I dive into a description of SAM's internal workings, I wanted to let you know about some theory involved. This is MY theory. It most likely fails to align with the theory used by the original author(s), but we will never know unless it magically appears in public some day. However, my theory is consistent with the program code.

On a more abstract level, the description of my theory probably violates some "laws" of phonetics, sampling theory, and/or information theory. In other words, it is how I think about SAM's speech and hope you find it helpful for your own understanding, but it may have some subtle "technical" flaws. (I'll produce a perfect theory if you pay me!)

I strive to use accurate terms, however, SAM's BASIC wedge (on the original C64 version) and its documentation refer to some settings by inappropriate terms (calling wavelength PITCH and time delay SPEED, for example). So I generally don't use the terms of the original version, or if I do, I try to make it obvious (with all caps shown in the last sentence) and phrase them alongside the correct terms. So just realize that sometimes I may sound like an idiot who doesn't know the difference between wavelength and frequency... but I do understand, and I'm trying to dance around the misconceptions introduced by the original.

SAM first translates input text (phonemes), through multiple steps, into a series of phones and, finally, into a series of F_Samples (for lack of a better term). These are used in the final stage to actually render audio on the computer's sound chip. Each "F_Sample" consists of:

a base wavelength
3 Formants
a type code

The base wavelength (or fundamental wavelength) is the inverse of the fundamental frequency. It is not directly rendered to the audio chip, however it affects the phase of all 3 formants (see below) that are rendered. It can also delay processing of a type code. The fundamental frequency controls the general pitch of speech (in contrast to the formants, which provide higher-frequency details). Note: I (mainly) use the term base wavelength, instead of frequency, because SAM does not manipulate the "fundamental" as a frequency, but as the reciprocal: time. I do not use a term like fundamental time period because this value actually does affect the pitch of speech (unlike some other SAM time periods which do not). Hopefully the term wavelength reminds you it is related to frequency/pitch and not duration/speed.

Each of the 3 Formants ("mouth", "throat", and undocumented) consists of two pieces of data: a frequency and a power/amplitude. Note that power is used for preliminary smoothing while amplitude is used for final rendering; I will use the term "volume" when I need to refer to both. Hopefully you see that each F_Sample has 6 values (besides type and base wavelength): F1.frequency, F1.volume, F2.frequency, F2.volume, F3.frequency, and F3.volume.

You may be wondering, "What is a Formant"? If you have time, check out this Wikipedia article. The short answer is: a Formant is an "important" waveform (for human listeners) with a specific frequency and volume. In SAM, the first two formants have a sine waveform. The third formant has a square waveform. The important thing to know is that each formant (of a phoneme) is assigned a specific frequency and volume... and each phoneme / F_Sample has 3 formants ("mouth", "throat", and undocumented).

The type code tells which method(s) are used to render the F_Sample. SAM will render an F_Sample with either (or both) of the following methods:

Formant (Fourier) compilation (adding multiple waveforms of various shape, frequency, and power/amplitude)
PCM rendering (quickly sending a large set of (two possible) amplitude values to the audio chip)

All vowels and most consonants are rendered with the Formant method. About 1/3 of consonants (the "rushing" ones) use pure PCM. A few consonants use a combination of both (Z, ZH, V, DH, and J).

Formant Rendering

So first a description of the most popular Formant method: it is related to Fourier transforms and similar techniques used in modern audio compression (and quite different from PCM). Each formant is described in terms of frequency and power/amplitude ("volume") . The amplitude of the 3 Formants are added together to produce the final audio output.

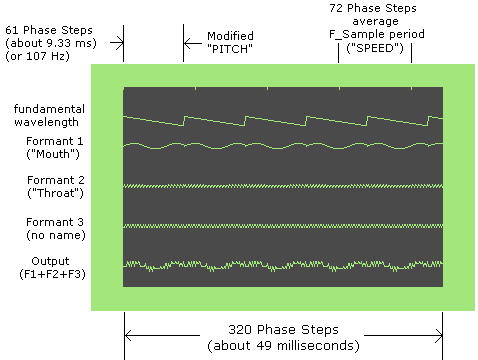
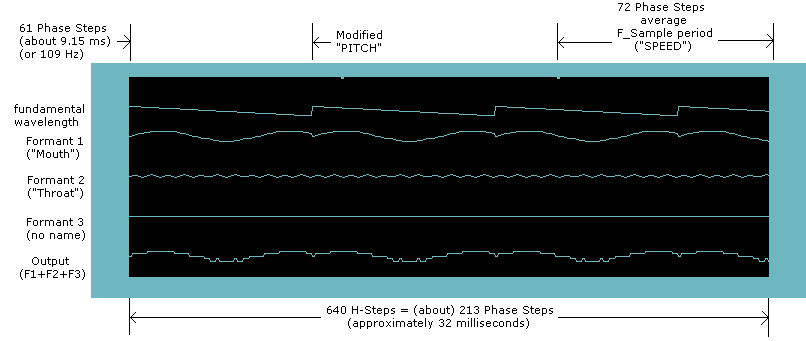
To clarify, I'll include some images which show the formants, base wavelength, and final output. For all of them, I used no stress on the phones and used SAM's default settings (in particular, PITCH=64 and SPEED=72). Although these images were captured from a Commodore 128 (in 40-column mode), SAM/Reciter does not generate graphs like these (it takes far too long to do in real-time). Let's start with an image showing the beginning of the NX phone:

Image of 3 formants, their sum, and fundamental wavelength for a period of 49 milliseconds at the beginning of phoneme NX.

A few things you should note:

The base wavelength (looks like a saw-wave near the top) is not added into the total output (shown at the bottom), but it affects pitch by resetting the phase of all three formants on a regular basis (it also controls acknowledgment of a new F_Sample's type).
You can see a little "dimple" in the sine wave of formant 1 every time its phase is reset by the fundamental wavelength.
The amplitude of formant 1 is a bit low, and really low for formants 2 and 3 (so low, you can't see the effect of phase-reset).
The output looks more noisy than it should -- the amplitude of each formant is 8 bits, but their sum is scaled down to 4 bits (due to the limits of bit-banging the SID audio chip).
There are about 5.25 cycles of the fundamental wavelength (err, frequency).

The base wavelength is calculated from three quantities. The first, most significant is the PITCH value. Second, a delta-wavelength value is added to this, based on Stress of the phoneme (this is usually a negative value, which means a stressed phoneme will have a shorter wavelength (higher frequency)). Since the phoneme is unstressed, and PITCH is 64, this gives a preliminary base wavelength of 64. The final quantity involved is the frequency of formant 1 ("mouth"). This value is divided by two and subtracted from the preliminary base wavelength to get the final base wavelength. Because the NX phone has a mouth frequency of 6, half that value (3) is subtracted from 64 to give a final base wavelength of 61. Mathematically,

base wavelength = PITCH + delta_wavelength(stress) - ( F1.Frequency / 2 )

Note 1: the resulting value of wavelength is in units of about 150 microseconds (assuming recommended TIMEBASE setting), which I simply call a phase step. The approximate frequency, in Hertz, is 6690 / wavelength. For the NX example, this means a fundamental frequency of 6690 / 61 = 110 Hz (approximately).

Note 2: the equation implies that PITCH + smallest used delta_wavelength should be greater than half the greatest "mouth" frequency (otherwise the wavelength will be less-than-or-equal-to zero and cause a wrap-around 256... for example, if the equation resulted in a value of -2, the wavelength would be 254 phase steps; a result of 0 would be 256 phase steps). If you use the greatest possible stress, then the smallest delta_wavelength is -32. If you use and the default KNOBS values, the greatest formant 1 frequency is 26. Thus PITCH - 32 > 26 / 2, or PITCH > 13 + 32, or PITCH > 45. If you used the maximum KNOBS "value-x" of 255, then maximum mouth frequency would be 51 (almost 26*2). In that case (and assuming most powerful stress) the relation becomes PITCH - 32 > 51 / 2, or PITCH > 25 + 32, or PITCH > 57.

Note 3: the equation makes no sense in terms of dimensional analysis! Adding PITCH (which is really a wavelength) to delta_wavelength gives us a wavelength (no problem), but then subtracting a frequency is just crazy! You can't really add or subtract wavelengths (err, time periods) with frequencies... it's like adding apples and oranges. For fun, ask a physics professor what you get when you subtract 3 Hz from 61 seconds.

The only reason it works (I'm guessing) is because the frequency is subtracted from the wavelength. So a higher mouth frequency will subtract more from the base wavelength than a moderate frequency. Subtracting more will generate a shorter fundamental wavelength... which means a higher fundamental frequency. I'm guessing this is some easy approximation to a more complex function.

The important thing to remember is the (final) base frequency will tend to track the frequency of formant 1, although it is mainly controlled by phoneme stress and the PITCH setting. Below are two more images to help show this.

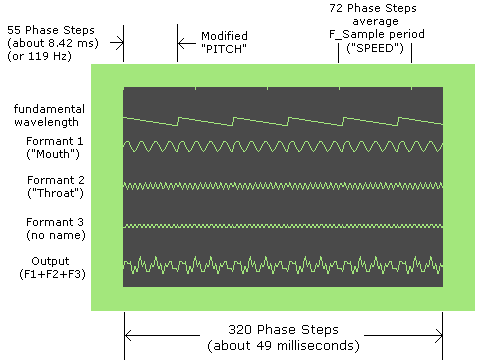
Next (second) is the beginning of the R phone. Because its "Mouth" frequency has a value of 18, the final base wavelength will be 64-18/2 = 55 phase steps. The base frequency will be about 6690 / 55 = 122 Hz (with the default PITCH and recommended TIMEBASE).

Image of 3 formants, their sum, and fundamental wavelength for a period of 49 milliseconds at the beginning of phoneme R.

In the R image, you should be able to see the effect of phase-reset on both formants 1 and 2 caused by the fundamental wavelength (they have a bit more amplitude than the very first NX image). You should also see that formant 3 still has a very low amplitude. You should now see 6 full cycles of the fundamental frequency (compared to 5.25 in the NX image) -- this is because the mouth frequency is greater in the R phoneme.

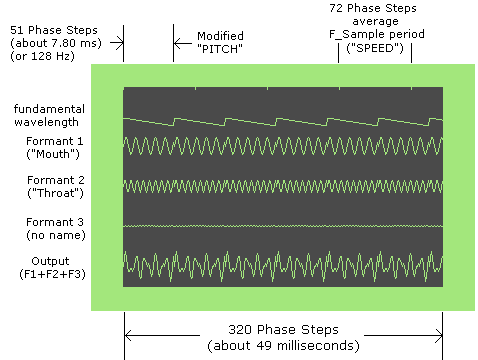
Next is the beginning of the (single) AW phoneme (it gets translated into two phones). Because its "Mouth" frequency has a value of 26 (at the beginning = first phone), the base wavelength will be 64-26/2 = 51 phase steps. The base frequency would be about 6690 / 51 = 131 Hz.

Image of 3 formants, their sum, and fundamental wavelength for a period of 49 milliseconds at the beginning of phoneme AW.

In the beginning-AW image, you should be able to see the phase-reset effect in all 3 formants on each cycle of the fundamental frequency. (Even though formant 3 has an incredibly low amplitude, you can see the effect if you look well). Formants 1 and 2 have a larger amplitude than any previous image (which makes seeing the phase-reset easy). Most important, you should see that now over 6 full cycles of the fundamental occurs (because the mouth frequency is higher than either R or NX).

F_Sample Period

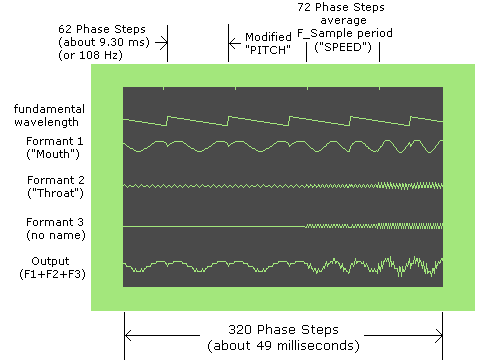
Along the top of the previous images (above the fundamental wavelength), you should see little tick marks. These indicate where the next F_Sample will be queued (prepared for play back). Now things get a bit tricky! The next F_Sample won't fully begin until the (current) fundamental frequency completes its cycle. The (fixed) distance between the marks represent the 'requested' hold time for samples, as set by SPEED.

With the default settings (SPEED slightly larger (longer) than PITCH (wavelength)), each F_Sample will alternate between 1 and 2 base wavelengths per sample. When a new F_Sample is queued, as indicated by the tick marks, SAM will immediately change all 3 formants to the new values of the next F_Sample. However, the base wavelength and "type" of the current F_Sample will remain in effect until the end of the current base wavelength.

SAM's algorithm implies the SPEED value should be the same or greater than the PITCH value, so that at least one full fundamental wavelength will play per F_Sample. (Because the fundamental wavelength will be a little shorter than the PITCH value, you could make SPEED one or two units smaller than PITCH.) In general, if the SPEED setting is lower than PITCH, then SAM will begin dropping some parts of F_Samples from the output (type and base wavelength). This will cause more abrupt changes in the fundamental frequency (base wavelength) which slightly lowers quality (speech smoothness). It may also trigger a bug with the PCM-only phonemes (I need to do more research).

In each of the images above, all the F_Samples were the same (which makes it impossible to see when a new F_Sample begins). When SAM first starts building the F_Samples from your input text, the same F_Sample is repeated for the duration of the phone (each phoneme/phone has one or two possible durations: natural and stressed). After all phones in a phrase have been "exploded" into a series of repeated F_Samples, SAM will modify some (or all) of the F_Samples around the transition between phones. For example, instead of having an abrupt change of frequencies, volumes and base wavelength between two phones, the components (frequency, volume, base wavelength) will smoothly change over a period of several F_Samples.

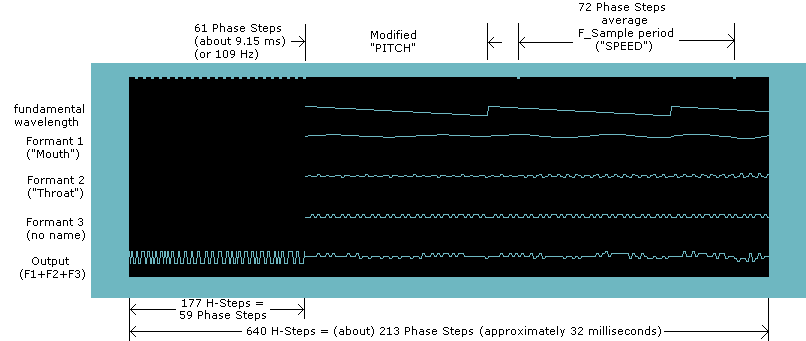
The following image shows the transition between the "M" and "IY" phones of the phonetic phrase "MIY".

Image of 3 formants, their sum, and fundamental wavelength for a period of 49 milliseconds in the middle of the phoneme-phrase "MIY" (phones M then IY).

The above image shows the F_Samples about 100 milliseconds after the start of the "MIY" phrase -- near the transition between the "M" and "IY" phones. Looking at Formant 1, it should be obvious where the phase reset occurs at each new base wavelength. Although it is a bit difficult, you can also see where a new frequency (in formant 1) occurs about 25% into the third FULL base wavelength (at the point of third tick-mark). To make things easier for you, look at the amplitude of Formants 2 and 3... at the same point in time, you should see an obvious increase in amplitude. You can also see another increase in amplitude of those formants about 50% into the fourth FULL base wavelength (at the point of the fourth tick-mark).

The import things to note are:

the frequency and amplitude of all 3 formants change on a "tick mark" (start of new F_Sample... determined by SPEED).
the F_Sample transition (tick mark) may occur anywhere inside the fundamental wavelength... look at the amplitude of formants 1 and 2,
although you can't easily see it, two things do NOT change (immediately) on a tick mark (F_Sample boundary):
1. The correct/new base wavelength won't take effect until the current (old) wavelength completes.
2. The correct/new F_Sample "type" won't take effect until the current (old) wavelength completes.
3. (Another example follows, to help if you are confused!)
phase-reset always occurs at the end of a base wavelength (regardless of where a new F_Sample (tick mark) occurs.

Hopefully you can see the "smooth" transition of frequency in Formant 1's waveform... and in the amplitude of Formants 2 and 3 (hard to see the frequency). The "smoothing" makes SAM sound more natural.

SAM does two types of smoothing. The fundamental wavelength is smoothed in an unbiased manner; at exactly 1/2 of the F_Samples of a phone, SAM generates a linear progression to the wavelength found at 1/2 of the F_Samples of the next phone. (A bit off-topic, each phone consists of n F_Samples where n is one of two values specific to its phoneme: natural duration or stressed duration.)

The 3 formants, on the other hand, are smoothed with a biased algorithm. For each pair of adjacent phones, this routine will compare a "dominance" value assigned to each phone. The more-dominant phone will have the same or (usually) fewer of its F_Samples altered than its less-dominant (subordinate) adjacent phone. For example, with a dominant phone before a subordinate one, the smoothing may begin during last 3 samples of the first phone and extend into the first 5 samples of the next phone. In particular, the last 3 samples of the first phone may be quite far from the center (for example if the phone was 12 F_Samples in duration, its center would be 6 F_Samples from the start of the next phone). Thus the more dominant phone has less of its samples smoothed, and the weaker phone has more samples altered. Anyway, once the biased start and end positions are determined, SAM once again generates a linear sequence of values between the start and end values (this is done 6 times: frequency and power of all three formants).

During the smoothing process, each formant in the F_Samples is composed of a frequency and a power. After smoothing, the power in the F_Samples is converted to amplitude using a simple look-up table.

Dual Rendering

This involves both PCM and Formant rendering of F_Samples. It applies to a few consonants (Z, ZH, V, DH, and J... see NOISES "Y-Values"). It is most similar to the Formant method, (described above) but the PCM samples radically alter the effect of base wavelength (PITCH) and duration (SPEED) which makes calculations (and description) quite tricky!

An important thing to note is that any PCM rendering (the currently discussed blended-method, or pure PCM) occurs at (approximately) 3x the "normal" rate used in the "pure" Formant rendering method (discussed above) -- assuming default TIMEBASE and NOISES settings. In order for me to adequately show this to you, I had to "expand" my images on the horizontal axis by a factor of three. Sadly, this made images of SAM's waveforms too "long" on the 40-column video screen. So I switched to 80-column mode for the following images...

To get you started, first is an image of an "normal" (pure Formant) rendering of phone (M):

Image of 3 formants, their sum, and fundamental wavelength for a period of 32 milliseconds at the beginning of phoneme M.

Hopefully you can see the similarities with the very first image above (NX phone). In particular, the base wavelength is 61 phase steps, the F_Sample period is 72 phase steps, you can see "dimples" (a phase-reset) in Formant 1's sine wave at each new base wavelength, and all the F_Samples are the same (no change in frequency or amplitude). The main differences to note are:

Although the graph is twice as wide (640 pixels), the total time period is shorter: about 32 milliseconds now (was about 49 milliseconds in prior images).
A single pitch step (about 150 microseconds) now measures 3 pixels wide (in prior images, it was 1 pixel wide)
A single pixel width now represents about 50 microseconds. I call this time period an H-Step (high-resolution) for lack of a better name.
This type of graph allows me to show you data with 3x greater frequency (3x shorter wavelength)
Although Formant 2 has a very low amplitude, you can see the waveform more clearly (because it is "magnified" on the horizontal axis)

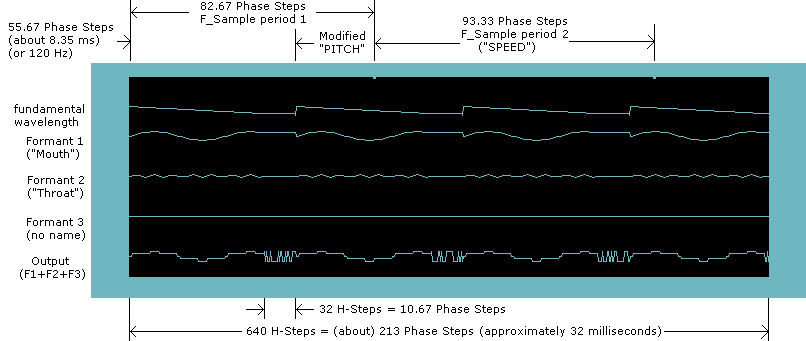
Next is an image showing actual dual rendering. It is the beginning of the V phone.

Image of 3 formants, their sum, and fundamental wavelength for a period of 32 milliseconds at the beginning of phoneme V.

There are several differences with the "dual" method to note (most of them you can see, for the rest, you'll have to take my word):

At the bottom of the graph (the Output), you will a short burst of high-frequency data ("noise") which occurs just prior to the end of each base wavelength.
The Output, during the burst, is generated solely from one of five PCM tables (specific to the current phone) -- the 3 formants are not involved
The 3 formants and the base wavelength show a "flat line" during the burst period because they are not updated (remain constant)
The "F_Sample counter", during the burst, is also not updated. You can't directly see the F_Sample counter in the graph, but you can see the effect of no-update: the F_Sample duration (distance between tick-marks, along the top) is extended by 10.67 phase-steps (in this example) for each "burst" of PCM. In particular, the first F_Sample happens to contain 1 burst, so it is extended once (from 72 to 82.67 phase steps), and the second F_Sample happens to contain 2 bursts, so it is extended twice (from 72 to 93.33 phase steps)

The purpose of the dual rendering method (my theory, of course) is to generate frequencies higher than are possible with the standard 3-formant method. From experience, I must say it does an effective job, however it should be obvious from the image that it fouls up two of the main components of audio: pitch and speed. I discuss each next.

The base wavelength represents the general pitch of a phone (or more precisely, an F_Sample within a phone). For the V phone in the above image, the base wavelength should have a value of 60. You can either peek into SAM's memory of F_Samples to verify this, or calculate it (with formula listed above) as 64-8/2 = 64-4 = 60 (the magic number 64 is the PITCH setting, and the magic number 8 is the "mouth" frequency of the "V" phone). However, as shown in the image, the actual wavelength is 7.2% less (55.67). This means a frequency/pitch slightly higher by about 7.8%. The formula to calculate a "dual" base wavelength (in units of phase-steps) is approximately:

dual_base_wavelength = int(standard_base_wavelength * 3/4) + 8 * [int(standard_base_wavelength / 16) + 1] / 3

The first addend in the formula represents 75% of the standard (3-formant method) base wavelength, rounded down (the "int" function). The second addend of the formula represents the time period for n PCM bytes (8n PCM samples). The number of PCM bytes is:

dual_PCM_bytes = int(standard_base_wavelength / 16) + 1

That is, 1/16 of the standard base wavelength (rounded down) plus one.

The F_Sample period controls the rate of speech (I think of it as the F_Sample hold period). Although the base wavelength has an imperfect compensation factor of 3/4, the F_Sample period has no compensation! Because there is no compensation, and SAM "forgets" to update its F_Sample counter during the burst of a dual-rendered phone, an F_Sample rendered with the dual method will be longer than requested by the SPEED setting. How much longer is almost random! As discussed previously (standard rendering), each F_Sample will generally consist of one or two base wavelengths (with default settings, SAM alternates between one and two such that average equals the requested SPEED value). For what it is worth, the approximate formula for a "dual" F_Sample's time period is:

(dual) F_Sample period = SPEED + n * 8 * dual_PCM_bytes / 3

where n is generally 1 or 2 (the number of dual_base_wavelengths which occur within an F_Sample).

The above image of the V phone shows this very well. The number of PCM bytes is 4 because int( 60/16 ) + 1 = 3 + 1. The first F_Sample, which contains one base wavelength, has a period of 72 + 1 * 8 * 4 / 3 = 82.67 phase-steps. The second F_Sample, which contains two base wavelengths, has a period of 72 + 2 * 8 * 4 / 3 = 93.33 phase-steps.

In summary, each F_Sample having a type of "dual rendering" will insert one or more bursts of (high-frequency) PCM samples. Each burst will occur after the first 75% of the phone is rendered with the standard (3-formant) method. The burst is rendered from one of five (256-byte) PCM tables (see NOISES "Y-values"), and will consist of a variable number of bytes (based on the standard base wavelength). The effective base wavelength will be shorter than standard (thus higher pitch), while the F_Sample's duration will be longer than standard (thus slower speech).

See, I told you the dual method is tricky!

One final technical note: the first PCM byte of the first "dual rendered" phone in a phrase will be a "random" value in the phone-specific PCM table. However, each subsequent PCM byte in the phone (or any following "dual rendered" phones) will be the next byte in the table. In effect, each burst will step through a PCM table just like the standard method steps through the phases of a sine wave. (However, the initial "psudo-phase" is random.)

A second technical note: each PCM byte encodes 8 PCM samples... that is, 1-bit PCM. The amplitude of each bit (0 or 1) is fixed for the dual rendering method (SID volume 6 or 10, respectively). More importantly, each bit is rendered for about 55 microseconds (using 1MHz/NTSC with default NOISES values)... this is only approximately 1/3 of a phase-step. So the images and equations for dual rendering are approximate. Otherwise (more precision) would require an even more expanded image and more complex formulas. If for some reason you want a more precise equation, then substitute the value "3" in the equations with the value "149.5 / 55" (2.718).

PCM Rendering

This uses "pure" PCM for an F_Sample. It applies to all "rushing" phonemes (S, SH, F, TH, /H, /X), and the second "sub-phoneme" of CH, P, and T. This rendering method completely ignores all three formants, the base wavelength, and the F_Sample period! One the one hand, it is boring because it is table-based (no variety). On the other hand, it fouls up the requested PITCH and SPEED in a rather complex way.

Because it relies on a table of PCM bytes, PCM rendering generates a fixed set of frequencies (ignores PITCH / base wavelength). Unlike the dual and standard methods of rendering, it also generates audio for a fixed time period (ignores SPEED / F_Sample period). I like to think of this rendering method as "pure noise", however, each phoneme has a specific PCM table to use, a specific initial phase, and a specific duration... so really it is psudo-noise... if you examine the data in the 5 PCM tables, you will notice a different mixture of frequencies in each.

Below is an image showing the transition between the pure PCM phone "CH" and the pure formant phone "IY". I didn't show all the PCM samples (because they would fill more than a full screen).

Image of "noise" followed by 3 formants, their sum, and fundamental wavelength for a period of 32 milliseconds at the transition between the phones "CH" and "IY".

As you can see (on the left third of the graph), the base wavelength and 3 formants are ignored (not updated or rendered) while the pure PCM samples are playing. The image shows a tick mark along the top for every PCM byte (every 8 PCM samples). This represents a reset of the F_Sample period... the image is a bit misleading because the F_Sample period is not actually reset on every PCM byte -- just after the last PCM byte. But the ultimate effect is the same: the F_Sample period and base wavelength (re)start as soon as the PCM samples finish playing.

If you want to calculate the duration of a "pure PCM" F_Sample, take the duration value (number of PCM bytes) from the NOISES "X-Values" then multiply by 8. This is the number PCM samples (or H-Steps as I like to refer to each time period). The duration is then approximately 50 microseconds times the number of PCM samples. Approximately 50 because that value is 1/3 of a phase-step (as shown in my wide graphs). The actual duration (using default NOISES on NTSC machine at 1MHz) is closer to 58 microseconds times the number of PCM samples. For the CH example, per the NOISES listing,, the number of PCM bytes is 112. So 1*112*8 = 896 PCM samples. The duration is approximately 50x that value (in microseconds), or 44.8 milliseconds. A more accurate calculation is 896 * 58 = 51968 microseconds, or about 52 milliseconds. Either way, you can see the duration is much longer than a typical ("normal rendered") F_Sample which has a duration around 72*150 = 10800 microseconds or about 11 milliseconds.

Don't forget that the actual phone consists of multiple F_Samples. To calculate the total duration of a phone, you normally multiply the F_Sample duration times the number of F_Samples in a phone (the duration column in the phoneme table). However, for "pure PCM" rendering, you have to divide the result by two. This is because whenever a "noisy" phone (pure PCM) is rendered, SAM will skip the next F_Sample in its sample buffer! All phones with a type of "pure PCM" are listed in the phoneme table with a duration of two. Some duration modification rules could extend the value, but (as far as I can tell) the result will always be a multiple of two. So SAM is (or rather should be) cutting off half the duration listed in its own tables for the "noisy" phone. Although the skipped F_Sample will be missing from the final output, it would be wrong to think it has no effect. The "missing" F_Sample will be used in the smoothing of F_Samples discussed earlier. By skipping it during the rendering stage, this results in a more abrupt transition. This seems silly to me, since the transition between PCM samples and 3-formant samples is already very abrupt!

The similarities of "pure" PCM Rendering with "burst" PCM (Dual Rendering) are:

A multiple of 8 PCM samples will be played, from one of five PCM tables
After the PCM samples finish playing, the base wavelength is reset
Each PCM sample plays for roughly 50 microseconds (more precisely, each "byte" (8 PCM samples) plays for about 450 microseconds)

The differences between the "pure" and "burst" methods include:

Pure PCM will always play the same sequence of bytes for a given phone (dual rendering will play the next set of bytes in the PCM table)
After the PCM samples finish playing, the pure PCM method will reset the F_Sample period (burst PCM will leave it alone)
Pure PCM rendering will always begin at the start of a base wavelength (burst PCM will start after 75% of the base wavelength)
Pure PCM will render each bit (PCM sample) for 58 microseconds (NOISES X-Value), while burst PCM will render each bit for 55 microseconds (NOISES Y-Value)
Pure PCM will discard the next F_Sample while burst PCM does not

Delayed Type and Base Wavelength

As discussed under Formant Rendering, the next F_Sample in a phrase may (and usually does) begin anywhere within a base wavelength. The frequency and amplitude of the three formants will take effect immediately, however the new F_Sample's type and base wavelength won't take effect until the start of the next base wavelength (or if you prefer, until the end of the current base wavelength). I don't know if this is a bug, or by design. Because the base wavelength doesn't immediately change, this helps SAM speak with a (slightly) more consistent pitch. Because the type doesn't change immediately, this can result in "confused rendering"; an F_Sample may play with the new/correct frequency and amplitude but with the wrong type. If this is not a bug, then I would say it is late-stage smoothing (as opposed to the normal, pre-render smoothing).

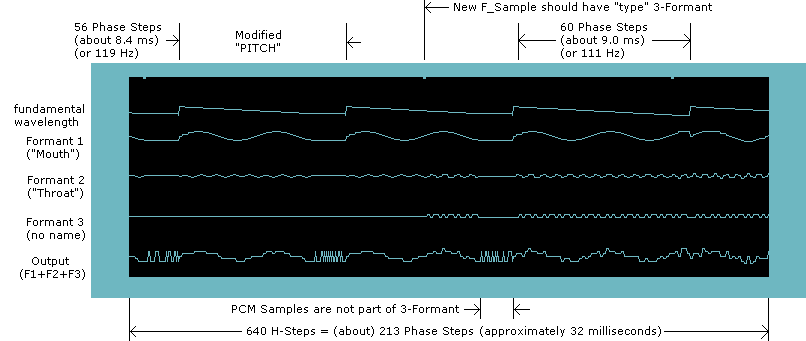
Below is an image of the transition between the "DH" and "IY" phones of the phrase "DHIY" to illustrate.

Image of 3 formants, their sum, and fundamental wavelength for a period of 32 milliseconds at the transition between DH and IY phones.

The image shows two complete F_Samples and three complete base wavelengths (plus fractional parts near the left and right borders). The first complete F_Sample is from then end of the Dual Rendered ("burst" PCM) phone "DH". The second complete F_Sample is from the start of the 3-formant phone "IY". In the first (complete) base wavelength (part of phone "DH"), you can see the base wavelength has a value of 56 phase-steps, a type of "burst PCM", and zero amplitude for Formant 3. In the third (complete) base wavelength (part of phone "IY"), you can see the base wavelength has a value of 60 phase-steps, a type of "3-Formant" (no PCM samples), and a non-zero amplitude for Formant 3.

Importantly, the central base wavelength shows "confused rendering" discussed above. Near the middle of the second (complete) base wavelength, the new F_Sample (for phone "IY") begins. All three fomants are updated immediately... it is not easy to see with Formants 1 and 2, but it should be obvious that Formant 3's amplitude increases from zero to some positive value. Although the new F_Sample updates the frequency and amplitude of the 3 formants instantly, the base wavelength remains at the old F_Sample value of 56 phase steps, and the type remains at the old F_Sample value of "burst PCM". Thus, you see a burst of 4 PCM bytes (32 PCM samples) at the end of the second (complete) base wavelength... even though SAM has begun the non-PCM (3-formant) rendering of the next F_Sample.

I'll explain why this happens (if you haven't figured it out) because it is not obvious from the image. The F_Sample type is "burst PCM" when the second (complete) base wavelength begins. Thus SAM will render a burst of PCM sample's after 75% of the base wavelength... despite the fact that a new F_Sample (of non-PCM type) begins near the middle (50%) of the base wavelength. In other words, the "type" of a (new) F_Sample is delayed (ignored) until the start of the next base wavelength.

This is a minor technical detail that, normally, I might not bother to mention and for which I definitely wouldn't construct a graphic image. However (as discussed under PCM Rendering), SAM should be cutting the last half of a "noisy" (pure PCM) phone. But because an F_Sample's type is not recognized (not "seen") by SAM until a new base wavelength begins, and because two F_Samples may "start" within a single base wavelength (only if you ignore the rule SPEED > PITCH), SAM may not see the first of a two-duration (two F_Samples) "noisy" phone. In this case, when the next base wavelength begins, SAM will render the second F_Sample as "noise" (pure PCM) and then skip the following (presumably non-noise) F_Sample. This (normally) just has the effect of cutting out a short transition (smoothing) F_Sample... or at least that is what I think the original authors intended! Unfortunately, there is a bug in the way this is coded in SAM... because the skipped F_Sample could be anything (and not part of the "noisy" phone as intended), SAM may skip the end-of-phrase!

If SAM skips the end-of-phrase, then it will play all remaining "junk" in its F_Sample buffer(s), then wrap around to the beginning and play it again. At the very least, this will sound terrible. At worst, it may result in an infinite loop! It would only result in an infinite loop if every pass of the F_Sample buffer resulted in two "noisy" F_Samples occurring in a single base wavelength right before the end-of-phrase. On the one hand, this seems unlikely because (generally) the base wavelength and F_Sample period are separate variables, and tend to drift relative to each other. On the other hand, as the image of the pure PCM rendering shows, the end of any "noisy" phone (pure PCM) will force an alignment of base wavelength and F_Sample period. So I believe (but have not tested) that if any "noisy" phones appear prior to the final, buggy, "noisy" phone, then an infinite loop will happen.

SAM's highest level

Here are some terms I invented that you need to know to makes sense of some of the following:

Vowel_X: a vowel, LX,RX,WX or YX.
volume: power or amplitude associated with a formant's frequency
F_Sample: a set of data consisting of a fundamental wavelength, formant data (3 pairs of frequency and volume), and a rendering type.

SAM is very shallow, in terms of subroutine nesting. He never goes more than 3 levels deep (4 if you include Reciter)! However, this does not mean he is simple. The code loops over the input (or derived versions thereof) many times. In fact, I am amazed it works in real-time on a 1MHz processor!

I go into detail below, but here are the main things SAM does:

Converts ASCII text into byte codes for phoneme and associated stress level (text -> phonemes)
Modifies some byte codes based on combination rules (phonemes -> phones)
Calculates duration (number of F_Samples) for each phone
Expands plosives and marks phrase boundaries (phones -> sub-phones)
Speaks all phrases

SAM Initialization

Regarding the first 4 steps, when you call SayItBASIC, SAM does the following:

Does hardware initialization (SID and usually VIC chip)
Saves important OS data (zero page values)
[Loop 1] Copies the BASIC string SA$ to SAM's text buffer (this step is skipped if you call SayIt: the non-BASIC version)
"Decode"

[Loop 2] Clears stress table
[Loop 3] Translates ASCII text into phoneme code and stress bytes (compress)

[Loop 4] Search and replace of certain (sets of) phoneme codes:

Expand diphthongs (AW, OW, UW, AY, EY, OY) to two phonemes (add WX or YX)
Translate (expand) shortcuts (UL, UM, UN) to two phonemes (AX + L/M/M)
(stressed vowel_x + space + stressed vowel_x) -> insert stop (Q)
Change (T + R) into (CH + R)
Change (D + R) into (J + R)
Change (vowel_x + R) into (vowel_x + RX)
Change (vowel_x + L) into (vowel_x + LX)
Change (G + S) into (G + Z)
Change K into KX if not followed by a vowel (followed by a consonant or punctuation)
Change G into GX if not followed by a vowel (followed by a consonant or punctuation)
Change (S + [P, T, K, KX]) into (S + [B, D, G, GX])
Change UW into UX if preceded by a dental/alveolar (DX, D, DH, T, TH, N, S, Z)
Expand affricates (CH and J) to two phonemes
Change D or T into DX if preceded by vowel_x and followed by stressed vowel_x (or space+vowel_x)

[Loop 5] Set stress level of each consonant followed immediately by a stressed vowel_x (value stress +1 = less stress)
[Loop 6] Initialize duration of each phoneme (one of two phoneme-specific values: stressed or normal)
[Loop 7] For each non-space punctuation mark, extend duration of preceding phonemes (except S, SH, F, TH) by 50% (back to and including a vowel_x).
[Loop 8] Search and modify the duration of certain pairs of phonemes. Once a modification is made, the code advances to the next phoneme before retesting. So generally, no more than 1 modification happens per phoneme. However, a nasal followed by two plosives will have the middle phoneme modified twice.

Extend duration by 25% of a vowel_x when followed by a voiced consonant.
Reduce duration by 12.5% of a vowel_x when followed by an unvoiced plosive (P, T, K, or KX).
Reduce duration by 1 (F_Sample) of a vowel_x when followed by: LX or RX then any consonant.
When a nasal (M,N,NX) is followed by a plosive, set the nasal's duration to 5 and the plosive's duration to 6.
When a plosive is followed by a plosive (possibly with intervening spaces), extend duration of both by 50% plus 1.
Reduce duration by 2 (F_Samples) of an approximant (L,R,W,Y) when preceded by a plosive.

[Loop 9] Expand plosives to the three phonemes (Catch,Hold,Release?) except unvoiced plosives followed by (ignoring spaces) /H, /X, or an occlusive (affricate, nasal, plosive, DX, or Q). The two added phonemes get their natural (unstressed) duration with the stress level (pitch control) of the original phoneme.
[Loop 10] Calculating a running total of duration values for phonemes. Reset the total and insert an end-of-phrase byte code (254) each time a non-space punctuation mark is found. If the running total exceeds 231 (including the punctuation's duration), then back-up to the previous space, change it to a glottal stop (Q), reset the total, and insert an end-of-phrase byte code. This step just flags phrase boundaries.
[Loop 12] Copy each phoneme's data (byte code, stress level, and duration) into 3 corresponding phrase buffers. When and end-of-phrase marker is found, write an end-of-string byte in the phrase buffer. When and end-of-phrase or end-of-string marker is found call SayPhrase and reset index to phrase buffer.
Restore OS data and (if needed) VIC hardware

Preparing to Speak a Phrase

Now that the simple(!) work has been done, we can prepare to render audio. Basically we need to build (8) tables of F_Sample data. Each F_Sample consists of:

Fundamental wavelength (# of phase steps before waveform reset)
Formant 1 ("Mouth") data: frequency and power
Formant 2 ("Throat") data: frequency and power
Formant 3 ("Lips/Tongue?") data: frequency and power
F_Sample type (usually 0, except for "noisy" sounds which use a PCM table)

Briefly, the following actions occur:

Calculate then replicate F_Sample data for each sub-phone in phrase (sub-phone -> F_Sample)
For any period or question mark, modify the preceding 30 F_Sample's fundamental wavelength
Smooth F_Samples which correspond with adjacent phonemes
Convert the F_Samples' power into amplitude
Play all F_Samples in the phrase

Regarding the first 4 steps, SAM does the following:

If the first phoneme in the phrase is end-of-string, then exit
[Loop 13] For each phoneme in phrase:

If the current phoneme is "." or "?" then

Set start-modify index to current F_Sample index less 30. (Or zero if underflow.)
Read the fundamental wavelength at the start-modify index. Call it the running wavelength.
For each F_Sample, from start-modify until (but not including) the punctuation mark, add +1 (if ".") or -1 (if "?") to the running total and save the value in the F_Sample's fundamental wavelength. (This causes pitch to fall if "." or rise if "?")

Use the current sub-phone's stress-level to lookup a delta_wavelength value.
Add delta_wavelength to PITCH to get the (preliminary) fundamental wavelength
[Loop 14] Repeat by the value stored in the phrase's duration (current sub-phone): Write the calculated fundamental wavelength; loop-up and write 3 formants' frequency and power data (per current sub-phone); look-up and write F_Sample type (per current sub-phone); advance to new F_Sample

Reset next F_Sample index
[Loop 15] For each sub-phone in phrase, except the last (this is the smoothing):

Calculate next F_Sample index = next F_Sample index + current sub-phone's duration
Compare the current sub-phone's "power" with the next sub-phone's "power"

If this sub-phone's power is greater, read this_tail_count from "phoModThis" table, and next_head_count from "phoModThat" table (both based on current sub-phone)
If next sub-phone's power is greater, read this_tail_count from "phoModThat" table, and next_head_count from "phoModThis" table (both based on next sub-phone)
If both have equal power, read this_tail_count from "phoModThis" table (based on this sub-phone), and next_head_count from "phoModThis" table (based on next sub-phone)

Set mod_start = next F_Sample index - this sub-phone's duration / 2.
Set mod_limit = next F_Sample index + next sub-phone's duration / 2.
Set total_count = wave_mod_limit - wave_mod_start
Set span = F_Sample[mod_limit].wavelength - F_Sample[mod_start].wavelength
Set step_size (quotient) = span / total_count, and step_rem (remainder) = remainder(span, total count)
Reset accumulator
[Loop 16] For each F_Sample from index = mod start until mod_limit -1 (this does "unbiased" wavelength smoothing)

Calculate new_value = F_Sample[current].wavelength + step_size
Calculate accumulator = accumulator + remainder
If accumulator >= span then add or subtract 1 from new value (depending on sign of span) and set accumulator = accumulator - span
Write new_value to F_Sample's wavelength

Set mod_start = next F_Sample index - this_tail_count
Set mod_limit = next F_Sample index + next_head_count
Set total_count = this_tail_count + next_head_count
[Loop 17] For each formant table (6 = 3*2) do this:

Set span = F_Sample[mod_limit].formant_data - F_Sample[mod_start].formant_data
Set step_size (quotient) = span / total_count, and step_rem (remainder) = remainder(span, total count)
Reset accumulator
[Loop 18] For each F_Sample from index = mod start until mod_limit -1 (this does "biased" formant smoothing)

Calculate new_value = F_Sample[current].formant_data + step_size
Calculate accumulator = accumulator + remainder
If accumulator >= span then add or subtract 1 from new value (depending on sign of span) and set accumulator = accumulator - span
Write new_value to F_Sample's formant_data

Calculate next F_Sample index = next F_Sample index + current (last) sub-phoneme's duration (index limit of all = number of F_Samples)
[Loop 19] For all F_Samples, reduce their fundamental wavelength by 1/2 of their Mouth (formant 1) frequency !!
[Loop 20] For each formants' volume (3) do this:

[Loop 21] For each F_Sample, look-up amplitude based on formant's power. Overwrite the formant's volume with amplitude value. (Amplitude = 16^power/16 * 18 / 16)

Enable I/O registers

Now all the F_Samples of the phrase are ready to be played! Note the value in "next F_Sample index" is the number of number of samples to play.

Now Speaking

All that remains is to render all the F_Samples in order. The final outer loop [Loop 22] does the following (in theory, once for each each F_Sample):

Set sample_hold = SPEED (see Poker)
[Loop 23] Do the following (until sample_hold = zero):

Set waveform_reset = F_Sample.wavelength
Set short_wave = 75% of F_Sample.wavelength
Reset phase of formants one, two, and three
Set pcm_type = F_Sample.type
If pcm_type AND 248 then call PlayPCMbits, increment F_Sample index, decrement number of samples remaining, and exit this loop (play Pure PCM)
Do the following (until waveform_reset = zero):

Wait 1 + 5 * TIMEBASE cycles (delay CPU)
Set accumulator = sine_value[formant1.phase] * F_Sample.formant1.amplitude
Add to accumulator: sine_value[formant2.phase] * F_Sample.formant2.amplitude
Add to accumulator: square_value[formant3.phase] * F_Sample.formant3.amplitude
Add to accumulator 136 ($88)
Divide accumulator by 16 and set as SID (audio chip) output value ($d418)
decrement sample_hold; if zero then exit two levels (this loop and parent)
decrement waveform_reset; if zero then exit (this loop)
decrement short_wave; if zero and pcm_type is not zero then call PlayPCMbitsA and exit this loop (play "burst" PCM)
Set formant1.phase = formant1.phase + F_Sample.formant1.frequency
Set formant2.phase = formant2.phase + F_Sample.formant2.frequency
Set formant3.phase = formant3.phase + F_Sample.formant3.frequency

Increment F_Sample index, decrement number of samples remaining
If number of samples remaining = 0 then exit loop

After the final loop ends (assuming it does), disable I/O registers and return to caller.

Notice the bug in the algorithm: for F_Samples of render type "Pure PCM", the number of samples remaining will be reduced by one but not tested (it could now be zero) -- this effectively skips the next F_Sample. When step 3 occurs, the remaining samples will be reduced again (if it was zero, it will now be 255). And when step 4 occurs, the test for end-of-F_Samples will fail (if the number of samples remaining wrapped to 255).

I think this bug got into the code because (as far as I can tell) the number of F_Samples per sub-phone of type "Pure PCM" is always an even number. And with the recommended setting of SPEED > PITCH, the "skipped" F_Sample will always be the second F_Sample of a "Pure PCM" pair. With those assumptions, the end-of-F_Samples would never be skipped. However, if the duration modification rules somehow created an odd-number of F_Samples for "Pure PCM" rendering (it doesn't seem possible, but I could have missed something) or if the PITCH > SPEED (which the user can easily do), then the skipped F_Sample may not be part of the "Pure PCM" sub-phone. If this happens on the very last F_Sample of a phrase, SAM will play all remaining "junk" in the F_Sample buffer, wrap around, and play the F_Sample buffer again (potential [very likely] infinite loop)!

One way to fix the bug is to enforce the rule SPEED > PITCH (and also verify duration rules could not generate an odd number of F_Samples of type PCM rendering). A lot of trouble. One easy fix is to simply test for zero after the first decrement (before returning to the outer loop for the second decrement and test). Another easy method is to never decrement the number of samples remaining; instead compare the current F_Sample index with the total number and exit if greater or equal. Not only does this solve the problem, it reduces the number of code bytes and increases render speed. Only minor problem with this method is the value for TIMEBASE would need to be increased due to the faster CPU execution (which is probably a good thing, because at 1MHz speed, the original TIMEBASE can't be decreased at all for PAL machines and only by 1 for NTSC machines... more variety would be nice).

Links

Project64 documentation of (C64) SAM.
Find out more about SAM+Reciter (C64) on Wikipedia!